समभुज चौकोनाचे क्षेत्रफळ किती असेल तर. समभुज चौकोनाचे क्षेत्रफळ कसे शोधायचे

- हा एक समांतरभुज चौकोन आहे, ज्यामध्ये सर्व बाजू समान असतात, नंतर सर्व समान सूत्रे समांतरभुज चौकोनासाठी लागू होतात, ज्यामध्ये उंची आणि बाजूच्या गुणाकाराद्वारे क्षेत्रफळ शोधण्याचे सूत्र समाविष्ट आहे.

समभुज चौकोनाचे क्षेत्रफळ त्याचे कर्ण जाणून घेऊनही शोधता येते. कर्ण समभुज चौकोनाला चार पूर्णपणे सारख्या काटकोन त्रिकोणात विभाजित करतात. जर आपण त्यांना आयत मिळवण्यासाठी क्रमवारी लावले तर त्याची लांबी आणि रुंदी एका पूर्ण कर्णाच्या आणि दुसऱ्या कर्णाच्या अर्ध्या भागाच्या समान असेल. म्हणून, समभुज चौकोनाच्या कर्णांचा गुणाकार करून समभुज चौकोनाचे क्षेत्रफळ दोनने कमी केले जाते (परिणामी आयताचे क्षेत्रफळ म्हणून).

फक्त कोन आणि बाजू उपलब्ध असल्यास, तुम्ही सहाय्यक म्हणून कर्णरेषाने स्वतःला हात लावू शकता आणि ज्ञात कोनाच्या विरुद्ध ते काढू शकता. मग ती समभुज चौकोनाला दोन समरूप त्रिकोणांमध्ये विभाजित करेल, ज्याचे एकूण क्षेत्र आपल्याला समभुज चौकोनाचे क्षेत्रफळ देईल. समद्विभुज त्रिकोणाचे क्षेत्रफळ म्हणून प्रत्येक त्रिकोणाचे क्षेत्रफळ बाजूच्या चौरसाच्या निम्म्या गुणाकाराच्या आणि ज्ञात कोनाच्या साइनच्या समान असेल. असे दोन त्रिकोण असल्याने, गुणांक रद्द होतात, फक्त बाजू दुसऱ्या अंशापर्यंत आणि साइन सोडतात:

जर समभुज चौकोनामध्ये वर्तुळ कोरलेले असेल, तर त्याची त्रिज्या 90° च्या कोनात असलेल्या बाजूस सूचित करेल, म्हणजे त्रिज्या समभुज चौकोनाच्या उंचीच्या दुप्पट असेल. मागील सूत्रात h=2r उंचीऐवजी बदलल्यास आपल्याला S=ha=2ra क्षेत्रफळ मिळते.

जर, कोरलेल्या वर्तुळाच्या त्रिज्यासह, बाजू नाही तर एक कोन दिलेला असेल, तर तुम्ही प्रथम उंची अशा प्रकारे रेखाटून बाजू शोधली पाहिजे की दिलेल्या कोनासह काटकोन त्रिकोण मिळेल. नंतर सूत्रानुसार त्रिकोणमितीय संबंधांमधून बाजू a शोधली जाऊ शकते . समभुज चौकोनाच्या क्षेत्रासाठी या अभिव्यक्तीला समान मानक सूत्रामध्ये बदलल्यास, असे दिसून येते

सर्व बाजू समान असलेला समांतरभुज चौकोन आहे.

काटकोन असलेल्या समभुज चौकोनाला चौरस म्हणतात आणि समभुज चौकोनाचा एक विशेष केस मानला जातो. आपण समभुज चौकोनाचे क्षेत्रफळ शोधू शकता वेगळा मार्ग, त्याचे सर्व घटक वापरून - बाजू, कर्ण, उंची. समभुज चौकोनाच्या क्षेत्रफळाचे क्लासिक सूत्र म्हणजे उंचीद्वारे मूल्याची गणना.

हे सूत्र वापरून समभुज चौकोनाचे क्षेत्रफळ मोजण्याचे उदाहरण अगदी सोपे आहे. आपल्याला फक्त डेटा प्लग इन करणे आणि क्षेत्राची गणना करणे आवश्यक आहे.

कर्णांच्या दृष्टीने समभुज चौकोनाचे क्षेत्रफळ

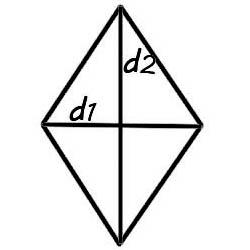
समभुज चौकोनाचे कर्ण काटकोनात छेदतात आणि छेदनबिंदूवर दुभाजक करतात.

कर्णांच्या दृष्टीने समभुज चौकोनाच्या क्षेत्रफळाचे सूत्र हे त्याच्या कर्णांना 2 ने भागलेले गुण आहे.

कर्णांमधून समभुज चौकोनाचे क्षेत्रफळ मोजण्याचे उदाहरण विचारात घ्या. कर्णांसह समभुज चौकोन द्यावा
d1 =5 सेमी आणि d2 =4. चला क्षेत्र शोधूया.

बाजूंच्या समभुज चौकोनाच्या क्षेत्रासाठीचे सूत्र इतर घटकांचा वापर देखील सूचित करते. जर वर्तुळ समभुज चौकोनात कोरलेले असेल, तर आकृतीचे क्षेत्रफळ बाजू आणि त्याच्या त्रिज्यावरून मोजले जाऊ शकते:

बाजूंनी समभुज चौकोनाचे क्षेत्रफळ मोजण्याचे उदाहरणही अगदी सोपे आहे. केवळ कोरलेल्या वर्तुळाची त्रिज्या मोजणे आवश्यक आहे. हे पायथागोरियन प्रमेय आणि सूत्राद्वारे प्राप्त केले जाऊ शकते.

समभुज चौकोनाचे क्षेत्रफळ एक बाजू आणि एक कोन

समभुज चौकोनाचे क्षेत्रफळ एका बाजूने आणि कोनातून काढण्याचे सूत्र बरेचदा वापरले जाते.

बाजू आणि कोनातून समभुज चौकोनाचे क्षेत्रफळ मोजण्याचे उदाहरण विचारात घ्या.

एक कार्य:समभुज चौकोन दिलेला आहे, ज्याचे कर्ण d1 \u003d 4 सेमी, d2 \u003d 6 सेमी आहेत. तीक्ष्ण कोपराα = 30° बरोबर. बाजू आणि कोन दिलेल्या आकृतीचे क्षेत्रफळ शोधा.
प्रथम, समभुज चौकोनाची बाजू शोधू. यासाठी आपण पायथागोरियन प्रमेय वापरतो. आपल्याला माहित आहे की छेदनबिंदूवर, कर्ण दुभाजक करतात आणि काटकोन तयार करतात. परिणामी:
मूल्ये बदला:
आता आपल्याला बाजू आणि कोन माहित आहे. चला क्षेत्र शोधूया:

भौमितिक क्षेत्र- या आकृतीचा आकार दर्शविणाऱ्या भौमितिक आकृतीचे संख्यात्मक वैशिष्ट्य (या आकृतीच्या बंद समोच्चाने बांधलेला पृष्ठभागाचा भाग). क्षेत्रफळाचा आकार त्यात असलेल्या चौरस एककांच्या संख्येने व्यक्त केला जातो.

त्रिकोण क्षेत्र सूत्रे

1. बाजू आणि उंचीसाठी त्रिकोण क्षेत्र सूत्र
   त्रिकोणाचे क्षेत्रफळत्रिकोणाच्या एका बाजूच्या लांबीच्या आणि या बाजूला काढलेल्या उंचीच्या लांबीच्या अर्ध्या गुणाप्रमाणे
   
2. त्रिकोणाच्या क्षेत्रफळाचे सूत्र तीन बाजू आणि परिक्रमा केलेल्या वर्तुळाची त्रिज्या
   
3. त्रिकोणाच्या क्षेत्रफळाचे सूत्र तीन बाजू आणि कोरलेल्या वर्तुळाची त्रिज्या दिली आहे
   त्रिकोणाचे क्षेत्रफळत्रिकोणाच्या अर्ध्या परिमितीच्या गुणाकार आणि अंकित वर्तुळाच्या त्रिज्याइतका आहे.
   
जेथे S हे त्रिकोणाचे क्षेत्रफळ आहे,
- त्रिकोणाच्या बाजूंची लांबी,
- त्रिकोणाची उंची,
- बाजूंमधील कोन आणि,
- कोरलेल्या वर्तुळाची त्रिज्या,
आर - परिक्रमा केलेल्या वर्तुळाची त्रिज्या,

चौरस क्षेत्र सूत्र

1. एका बाजूची लांबी दिल्यास चौकोनाच्या क्षेत्रफळाचे सूत्र
   चौरस क्षेत्रत्याच्या बाजूच्या लांबीच्या चौरसाइतकी आहे.
2. कर्णाची लांबी दिल्यास चौकोनाच्या क्षेत्रफळाचे सूत्र
   चौरस क्षेत्रत्याच्या कर्णाच्या लांबीच्या अर्ध्या चौरसाच्या समान.
   

   एस =	1	2
   	2

जेथे S हे चौरसाचे क्षेत्रफळ आहे,
चौरसाच्या बाजूची लांबी आहे,
चौरसाच्या कर्णाची लांबी आहे.

आयत क्षेत्र सूत्र

आयत क्षेत्रत्याच्या दोन लगतच्या बाजूंच्या लांबीच्या गुणाकाराच्या समान आहे

जेथे S हे आयताचे क्षेत्रफळ आहे,
आयताच्या बाजूंच्या लांबी आहेत.

समांतरभुज चौकोनाच्या क्षेत्रासाठी सूत्रे

1. बाजूची लांबी आणि उंचीसाठी समांतरभुज चौकोन क्षेत्र सूत्र
   समांतरभुज चौकोन क्षेत्र
2. समांतरभुज चौकोनाच्या क्षेत्रफळाचे सूत्र दोन बाजू आणि त्यांच्यामधील कोन दिले आहे
   समांतरभुज चौकोन क्षेत्रत्‍याच्‍या बाजूच्‍या लांबीच्‍या गुणाकार त्‍यांच्‍यामधील कोनाच्‍या साइनने गुणाकार केल्‍यास समान आहे.
   

   a b sinα

जेथे S हे समांतरभुज चौकोनाचे क्षेत्रफळ आहे,
समांतरभुज चौकोनाच्या बाजूंच्या लांबी आहेत,
समांतरभुज चौकोनाची उंची आहे,
समांतरभुज चौकोनाच्या बाजूंमधील कोन आहे.

समभुज चौकोनाच्या क्षेत्रासाठी सूत्रे

1. समभुज चौकोनाचे क्षेत्र सूत्र दिलेले बाजूची लांबी आणि उंची
   समभुज चौकोन क्षेत्रत्याच्या बाजूच्या लांबीच्या गुणाकाराच्या आणि या बाजूला कमी केलेल्या उंचीच्या लांबीच्या समान आहे.
2. समभुज चौकोनाच्या क्षेत्रफळाचे सूत्र बाजूची लांबी आणि कोन दिले आहे
   समभुज चौकोन क्षेत्रत्याच्या बाजूच्या लांबीच्या चौरसाच्या गुणाकार आणि समभुज चौकोनाच्या बाजूंमधील कोनाच्या साइनच्या गुणाप्रमाणे आहे.
3. समभुज चौकोनाच्या कर्णांच्या लांबीवरून त्याच्या क्षेत्रफळाचे सूत्र
   समभुज चौकोन क्षेत्रत्याच्या कर्णांच्या लांबीच्या अर्ध्या गुणाप्रमाणे आहे.
जेथे S हे समभुज चौकोनाचे क्षेत्रफळ आहे,
- समभुज चौकोनाच्या बाजूची लांबी,
- समभुज चौकोनाच्या उंचीची लांबी,
- समभुज चौकोनाच्या बाजूंमधील कोन,
1, 2 - कर्णांची लांबी.

ट्रॅपेझियम क्षेत्र सूत्रे

1. ट्रॅपेझॉइडसाठी हेरॉनचे सूत्र

   जेथे S हे ट्रॅपेझॉइडचे क्षेत्रफळ आहे,
   - ट्रॅपेझॉइडच्या पायाची लांबी,
   - ट्रॅपेझॉइडच्या बाजूंची लांबी,
   

समभुज चौकोन ही भूमितीतील एक विशेष आकृती आहे. त्याच्या विशेष गुणधर्मांमुळे, समभुज चौकोनाचे क्षेत्रफळ मोजणारे एक नाही तर अनेक सूत्रे आहेत. हे गुणधर्म काय आहेत आणि या आकृतीचे क्षेत्रफळ शोधण्यासाठी सर्वात सामान्य सूत्रे कोणती आहेत? चला ते बाहेर काढूया.

कोणत्या भौमितिक आकृतीला समभुज चौकोन म्हणतात

समभुज चौकोनाचे क्षेत्रफळ काय आहे हे जाणून घेण्यापूर्वी, ते कोणत्या प्रकारची आकृती आहे हे जाणून घेणे योग्य आहे.

युक्लिडियन भूमितीच्या काळापासून, समभुज चौकोनाला सममितीय चतुर्भुज म्हटले जाते, ज्याच्या चारही बाजू लांबीच्या समान आणि जोड्यांमध्ये समांतर असतात.

शब्दाची उत्पत्ती

या आकड्याचे नाव बहुमतात आले आधुनिक भाषाग्रीकमधून, लॅटिनच्या मध्यस्थीद्वारे. "समभुज" या शब्दाचा "पूर्वज" ग्रीक संज्ञा ῥόμβος (टंबोरिन) होता. जरी विसाव्या शतकातील रहिवासी, गोलाकार टॅंबोरिनची सवय असले तरी, त्यांची वेगळ्या स्वरूपात कल्पना करणे कठीण आहे, परंतु हेलेन्समध्ये हे संगीत वाद्येपारंपारिकपणे गोलाकार नसून हिऱ्याच्या आकाराचे बनवले जाते.

बहुतेक आधुनिक भाषांमध्ये, ही गणिती संज्ञा लॅटिनमध्ये वापरली जाते: रॉम्बस. तथापि, मध्ये इंग्रजी भाषाकधीकधी समभुज चौकोनांना डायमंड (हिरा किंवा हिरा) म्हणतात. या आकृतीला त्याच्या विशेष आकारामुळे असे टोपणनाव मिळाले, त्याची आठवण करून दिली रत्न. नियमानुसार, समान संज्ञा सर्व समभुज चौकोनांसाठी वापरली जात नाही, परंतु केवळ त्यांच्यासाठी वापरली जाते ज्यात त्याच्या दोन बाजूंच्या छेदनबिंदूचा कोन साठ किंवा पंचेचाळीस अंश आहे.

पहिल्या शतकात राहणाऱ्या एका ग्रीक गणितज्ञाच्या लिखाणात या आकृतीचा प्रथम उल्लेख करण्यात आला होता नवीन युग- अलेक्झांड्रियाचा हेरॉन.

या भौमितिक आकृतीचे गुणधर्म काय आहेत

समभुज चौकोनाचे क्षेत्रफळ शोधण्यासाठी, प्रथम आपल्याला दिलेल्या भूमितीय आकृतीमध्ये कोणती वैशिष्ट्ये आहेत हे जाणून घेणे आवश्यक आहे.

समांतरभुज चौकोन कोणत्या परिस्थितीत समभुज चौकोन असतो?

तुम्हाला माहिती आहे की, प्रत्येक समभुज चौकोन समांतरभुज चौकोन असतो, परंतु प्रत्येक समांतरभुज चौकोन समभुज चौकोन नसतो. सादर केलेली आकृती खरोखरच समभुज चौकोन आहे, आणि साधा समांतरभुज चौकोन नाही हे अचूकपणे सांगण्यासाठी, ते समभुज चौकोनाला वेगळे करणाऱ्या तीन मुख्य वैशिष्ट्यांपैकी एकाशी संबंधित असणे आवश्यक आहे. किंवा तिन्ही एकाच वेळी.

1. समांतरभुज चौकोनाचे कर्ण नव्वद अंशाच्या कोनात छेदतात.
2. कर्ण त्यांचे दुभाजक म्हणून काम करून कोपऱ्यांना दोन भागात विभागतात.
3. केवळ समांतरच नाही तर लगतच्या बाजूंचीही लांबी समान असते. हे, तसे, समभुज चौकोन आणि समांतरभुज चौकोनातील मुख्य फरकांपैकी एक आहे, कारण दुसर्‍या आकृतीची समान लांबी फक्त समांतर बाजू आहे, परंतु समीप बाजू नाही.

समभुज चौकोन कोणत्या परिस्थितीत चौरस असतो?

त्याच्या गुणधर्मांनुसार, काही प्रकरणांमध्ये, समभुज चौकोन एकाच वेळी चौरस बनू शकतो. या विधानाची दृष्यदृष्ट्या पुष्टी करण्यासाठी, स्क्वेअरला कोणत्याही दिशेने पंचेचाळीस अंशांनी फिरवणे पुरेसे आहे. परिणामी आकृती समभुज चौकोन असेल, ज्याचा प्रत्येक कोपरा नव्वद अंशांच्या बरोबरीचा असेल.

तसेच, चौरस समभुज चौकोन आहे याची पुष्टी करण्यासाठी, तुम्ही या आकृत्यांच्या चिन्हांची तुलना करू शकता: दोन्ही प्रकरणांमध्ये, सर्व बाजू समान आहेत आणि कर्ण हे दुभाजक आहेत आणि नव्वद अंशांच्या कोनात छेदतात.

समभुज चौकोनाचे कर्ण वापरून त्याचे क्षेत्रफळ कसे शोधायचे

एटी आधुनिक जगइंटरनेटवर आपल्याला आवश्यक गणना करण्यासाठी जवळजवळ सर्व साहित्य सापडेल. तर, विशिष्ट आकृतीचे क्षेत्रफळ आपोआप मोजण्यासाठी प्रोग्राम्ससह भरपूर संसाधने आहेत. शिवाय, जर (समभुज चौकोनाच्या बाबतीत) यासाठी अनेक सूत्रे असतील, तर कोणते वापरणे सर्वात सोयीचे असेल ते निवडणे शक्य आहे. तथापि, सर्व प्रथम, आपण स्वत: संगणकाच्या मदतीशिवाय समभुज चौकोनाचे क्षेत्रफळ मोजण्यात आणि सूत्रे नेव्हिगेट करण्यास सक्षम असणे आवश्यक आहे. समभुज चौकोनासाठी त्यापैकी बरेच आहेत, परंतु त्यापैकी सर्वात प्रसिद्ध चार आहेत.

या आकृतीचे क्षेत्रफळ शोधण्याचा सर्वात सोपा आणि सामान्य मार्ग म्हणजे तुम्हाला त्याच्या कर्णांच्या लांबीबद्दल माहिती असल्यास. समस्येमध्ये हा डेटा असल्यास, या प्रकरणात, आपण क्षेत्र शोधण्यासाठी खालील सूत्र लागू करू शकता: S = KM x LN / 2 (KM आणि LN हे KLMN समभुज चौकोनाचे कर्ण आहेत).

तुम्ही या सूत्राची वैधता व्यवहारात तपासू शकता. समजा की KLMN समभुज चौकोनाची लांबी त्याच्या कर्णांपैकी एक KM - 10 सेमी, आणि दुसरा LN - 8 सेमी आहे. मग आम्ही या डेटाला वरील सूत्रामध्ये बदलतो आणि आम्हाला पुढील परिणाम मिळतो: S \u003d 10 x 8 / 2 \u003d 40 सेमी 2.

समांतरभुज चौकोनाचे क्षेत्रफळ मोजण्याचे सूत्र

आणखी एक सूत्र आहे. समभुज चौकोनाच्या व्याख्येत वर नमूद केल्याप्रमाणे, तो केवळ चतुर्भुज नसून समांतरभुज चौकोन देखील आहे आणि या आकृतीची सर्व वैशिष्ट्ये त्यात आहेत. या प्रकरणात, त्याचे क्षेत्रफळ शोधण्यासाठी, समांतरभुज चौकोनासाठी वापरलेले सूत्र वापरणे योग्य आहे: S \u003d KL x Z. या प्रकरणात, KL समांतरभुज चौकोनाच्या बाजूची लांबी आहे (समभुज चौकोन), आणि Z आहे या बाजूला काढलेल्या उंचीची लांबी.

काही समस्यांमध्ये, बाजूची लांबी दिली जात नाही, परंतु समभुज चौकोनाची परिमिती ज्ञात आहे. ते शोधण्याचे सूत्र वर सूचित केले असल्याने, ते बाजूची लांबी शोधण्यासाठी देखील वापरले जाऊ शकते. तर, आकृतीची परिमिती 10 सेमी आहे. परिमिती सूत्र उलट करून आणि 10 ने 4 विभाजित करून बाजूची लांबी शोधली जाऊ शकते. परिणाम 2.5 सेमी असेल - ही समभुज चौकोनाची इच्छित बाजूची लांबी आहे.

बाजूला काढलेल्या उंचीची लांबी देखील 2.5 सेमी आहे हे जाणून आता या संख्येला सूत्रामध्ये बदलण्याचा प्रयत्न करणे फायदेशीर आहे. आता ही मूल्ये वरील सूत्रामध्ये क्षेत्रफळासाठी ठेवण्याचा प्रयत्न करूया. u200b समांतरभुज चौकोन. असे दिसून आले की समभुज चौकोनाचे क्षेत्रफळ S = 2.5 x 2.5 = 6.25 सेमी 2 आहे.

समभुज चौकोनाचे क्षेत्रफळ मोजण्याचे इतर मार्ग

ज्यांनी आधीच सायन्स आणि कोसाइनमध्ये प्रभुत्व मिळवले आहे ते समभुज चौकोनाचे क्षेत्रफळ शोधण्यासाठी त्यात असलेली सूत्रे वापरू शकतात. एक उत्कृष्ट उदाहरण खालील सूत्र आहे: S = KM 2 x Sin KLM. या प्रकरणात, आकृतीचे क्षेत्र समभुज चौकोनाच्या दोन बाजूंच्या गुणाकाराच्या समान असते, त्यांच्या दरम्यानच्या कोनाच्या साइनने गुणाकार केला जातो. आणि समभुज चौकोनात सर्व बाजू सारख्याच असल्याने, सूत्रात दाखविल्याप्रमाणे, एका बाजूस त्वरित चौकोन करणे सोपे आहे.

आम्ही ही योजना व्यवहारात तपासतो, आणि केवळ समभुज चौकोनालाच नाही, तर एका चौरसावर, ज्यामध्ये तुम्हाला माहिती आहे, सर्व कोन बरोबर आहेत, याचा अर्थ ते नव्वद अंशांच्या समान आहेत. समजा बाजूंपैकी एक 15 सेमी आहे. हे देखील ज्ञात आहे की 90 ° च्या कोनाची साइन एक समान आहे. नंतर, सूत्रानुसार, S \u003d 15 x 15 x सिन 90 ° \u003d 255x1 \u003d 255 सेमी 2.

वरील व्यतिरिक्त, काही प्रकरणांमध्ये, समभुज चौकोनाचे क्षेत्रफळ निश्चित करण्यासाठी साइन वापरून दुसरे सूत्र वापरले जाते: S \u003d 4 x R 2 / Sin KLM. या आवृत्तीत, समभुज चौकोनात कोरलेल्या वर्तुळाची त्रिज्या वापरली आहे. हे चौरसाच्या बळापर्यंत वाढवले ​​जाते आणि चारने गुणाकार केले जाते. आणि संपूर्ण परिणाम कोरलेल्या आकृतीला लागून असलेल्या कोनाच्या साइनने विभागला जातो.

उदाहरण म्हणून, गणनेच्या साधेपणासाठी, पुन्हा एक चौरस घेऊ (त्याच्या कोनाची साइन नेहमी एक असेल). त्यामध्ये कोरलेल्या वर्तुळाची त्रिज्या 4.4 सेमी आहे. नंतर समभुज चौकोनाचे क्षेत्रफळ खालीलप्रमाणे मोजले जाईल: S \u003d 4 x 4.4 2 / Sin 90 ° \u003d 77.44 cm 2

समभुज चौकोनाची त्रिज्या शोधण्यासाठी वरील सूत्रे त्यांच्या प्रकारातील एकमेव सूत्रांपासून दूर आहेत, परंतु ते समजणे आणि गणना करणे सर्वात सोपी आहे.

समभुज चौकोन हे समांतरभुज चौकोनाचे विशेष प्रकरण आहे. ही एक सपाट चौकोनी आकृती आहे ज्यामध्ये सर्व बाजू समान आहेत. हा गुणधर्म निर्धारित करतो की समभुज चौकोनांना समांतर विरुद्ध बाजू आणि समान विरुद्ध कोन असतात. समभुज चौकोनाचे कर्ण काटकोनात छेदतात, त्यांच्या छेदनबिंदूचा बिंदू प्रत्येक कर्णाच्या मध्यभागी असतो आणि ज्या कोनातून ते बाहेर पडतात ते कोन अर्ध्या भागात विभागलेले असतात. म्हणजे, ते समभुज चौकोनाचे कर्ण आहेत ते कोनांचे दुभाजक आहेत. वरील व्याख्या आणि समभुज चौकोनांच्या सूचीबद्ध गुणधर्मांच्या आधारे, त्यांचे क्षेत्र विविध प्रकारे निर्धारित केले जाऊ शकते.

1. समभुज चौकोनाचे AC आणि BD दोन्ही कर्ण ज्ञात असल्यास, समभुज चौकोनाचे क्षेत्रफळ कर्णांच्या गुणाकाराच्या निम्मे म्हणून निर्धारित केले जाऊ शकते.

S = ½ ∙ एसी ∙ बी.डी

जेथे AC, BD ही समभुज चौकोनाच्या कर्णांची लांबी आहे.

हे असे का आहे हे समजून घेण्यासाठी, आपण समभुज चौकोनात आयत अशा प्रकारे लिहू शकता की नंतरच्या बाजू समभुज चौकोनाच्या कर्णांना लंब असतील. हे स्पष्ट होते की समभुज चौकोनाचे क्षेत्रफळ अशा प्रकारे समभुज चौकोनात कोरलेल्या आयताच्या अर्ध्या क्षेत्रफळाइतके असेल, ज्याची लांबी आणि रुंदी समभुज चौकोनाच्या कर्णांच्या आकाराशी सुसंगत असेल.

2. समांतर पट्टीशी साधर्म्य दाखवून, समभुज चौकोनाचे क्षेत्रफळ त्याच्या बाजूचे गुणाकार म्हणून शोधले जाऊ शकते, विरुद्ध बाजूपासून दिलेल्या लंबाच्या उंचीवरून खाली दिलेल्या बाजूने.

S = a ∙ h

जेथे a समभुज चौकोनाची बाजू आहे;
h ही दिलेल्या बाजूस सोडलेल्या लंबाची उंची आहे.

3. समभुज चौकोनाचे क्षेत्रफळ त्याच्या बाजूच्या चौरस कोनाच्या α ने गुणिले जाते.

S = a2 ∙ पाप α

जेथे, a समभुज चौकोनाची बाजू आहे;
α हा बाजूंमधील कोन आहे.

4. तसेच, समभुज चौकोनाचे क्षेत्रफळ त्याच्या बाजूने आणि त्यात कोरलेल्या वर्तुळाची त्रिज्या शोधता येते.

S=2 ∙ a ∙ आर

जेथे, a समभुज चौकोनाची बाजू आहे;
r ही समभुज चौकोनात कोरलेल्या वर्तुळाची त्रिज्या आहे.

मनोरंजक माहिती
समभुज चौकोन हा शब्द प्राचीन ग्रीक रॉम्बसपासून आला आहे, ज्याचा अर्थ "टंबोरिन" आहे. त्या दिवसांत, टंबोरिनला खरोखरच हिऱ्याचा आकार होता, गोल नाही, कारण सध्या आपल्याला ते पाहण्याची सवय आहे. तेव्हापासून, कार्ड सूटचे नाव "टंबोरिन" देखील आले आहे. खूप रुंद समभुज चौकोन विविध प्रकारचेहेराल्ड्री मध्ये वापरले.